簡易
leetcode79

Problem

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

!https://assets.leetcode.com/uploads/2020/11/07/search1.jpg

1
2
3
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

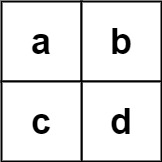
!https://assets.leetcode.com/uploads/2020/11/07/search2.jpg

1
2
3
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 12
  • board[i][j] is a lowercase English letter.
  • 1 <= words.length <= 3 * 10^4
  • 1 <= words[i].length <= 10
  • words[i] consists of lowercase English letters.
  • All the strings of words are unique.

Solve

Trie

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
# 先建立一個Trie，再用DFS去找
class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, word):
        node = self.root
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.is_word = True
    
    def search(self, word):
        node = self.root
        for char in word:
            if char not in node.children:
                return False
            node = node.children[char]
        return node.is_word

    def startsWith(self, prefix):
        node = self.root
        for char in prefix:
            if char not in node.children:
                return False
            node = node.children[char]
        return True

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:

        # 如果board是空的，或是board裡面的row是空的，就直接回傳空的list
        if not board or not board[0]:
            return []

        # 建立一個Trie
        trie = Trie()
        # 把words裡面的word都insert進去
        for word in words:
            trie.insert(word)
        
        # 建立一個res來存答案
        res = []

        # 用DFS去找
        def dfs(i, j, node, path):
            char = board[i][j]
            if char not in node.children:
                return
            
            # node.children[char]是下一個node
            next_node = node.children[char]
            
            # 如果next_node是word，就把path + char加進res裡面
            if next_node.is_word:
                res.append(path + char)
                next_node.is_word = False  # 避免重複加入

            board[i][j] = "#"  # 標記已經走過了

            # 用DFS遍地搜尋
            for x, y in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                new_i, new_j = i + x, j + y
                # 如果new_i, new_j在board裡面，就繼續DFS
                if 0 <= new_i < len(board) and 0 <= new_j < len(board[0]):
                    dfs(new_i, new_j, next_node, path + char)

            board[i][j] = char  # 回復

        # 用DFS去搜尋所有的board
        # 這邊的i, j是board的row, col
        for i in range(len(board)):
            for j in range(len(board[0])):
                dfs(i, j, trie.root, "")
        return res

易讀版

Trie 的 search, startsWith事實上沒有用到，所以可以不用寫

看解答有人多寫一個 removeWord，這樣 is_word 就不用改成 False，更好理解，也會比較快

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, word):
        node = self.root
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.is_word = True

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        node = Trie()
        for word in words:
            node.insert(word)
        
        res = []

        def dfs( r , c , node , path):

            if (r < 0 
            or r >= len(board) 
            or c < 0 
            or c >= len(board[0]) 
            ):
                return 

            char = board[r][c]
            if char not in node.children:
                return

            if node.children[char].is_word:
                res.append(path + char)
                node.children[char].is_word = False

            board[r][c] = "#"

            dfs( r+1 , c , node.children[char] , path + char)
            dfs( r-1 , c , node.children[char] , path + char)
            dfs( r , c+1 , node.children[char] , path + char)
            dfs( r , c-1 , node.children[char] , path + char)
            
            board[r][c] = char

        for r in range(len(board)):
            for c in range(len(board[0])):
                dfs( r , c , node.root , "")
        return res