Problem

You are given an m x n integer matrix matrix with the following two properties:

  • Each row is sorted in non-decreasing order.
  • The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

!https://assets.leetcode.com/uploads/2020/10/05/mat.jpg

1
2
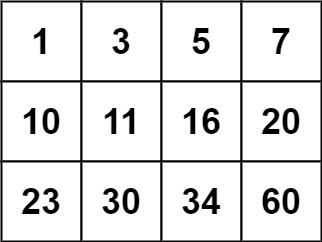
3
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

!https://assets.leetcode.com/uploads/2020/10/05/mat2.jpg

1
2
3
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • 10^4 <= matrix[i][j], target <= 10^4

Solve

這題一樣就binary search

法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:

        m , n = len(matrix), len(matrix[0])

        left = 0
        right = m*n -1

        while left <= right :
            mid = (left + right) // 2
            mid_val = matrix[ mid // n][mid % n ]
            
            if mid_val == target:
                return True
            elif mid_val < target :
                left = mid + 1
            else :
                right = mid  - 1

        return False

Time Complexity: O(log(mn))

Space Complexity: O(1)

法2

比第一種還快些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:

        m , n = len(matrix), len(matrix[0])

        left = 0
        right = m - 1 

        while left <= right:
            mid = (left + right) // 2
            mid_val = matrix[mid][0]
            if target == mid_val:
                return True
            else if mid_val < target :
                left = mid + 1
            else :
                right = mid  - 1

        # row 選擇的是比target小的最大值
        row = right

        left2 = 0
        right2 = n - 1

        while left2 <= right2:
            mid2 = (left2 + right2) // 2
            mid_val2 = matrix[row][mid2]
            if target == mid_val2:
                return True
            else if mid_val2 < target :
                left2 = mid2 + 1
            else :
                right2 = mid2  - 1
            
        return False

Time Complexity: O(log(m) + log(n))

Space Complexity: O(1)

O(log(m) + log(n)) < O(log(mn))

所以第二種方法比較快