Problem

There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.

You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.

A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.

Team a will be the champion of the tournament if there is no team b that is stronger than team a.

Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.

Notes

  • A cycle is a series of nodes a1, a2, ..., an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, ..., an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
  • A DAG is a directed graph that does not have any cycle.

Example 1:

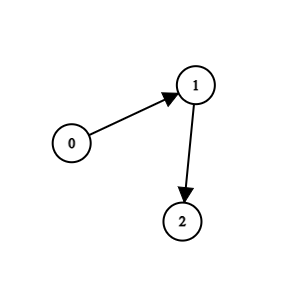
!https://assets.leetcode.com/uploads/2023/10/19/graph-3.png

1
2
3
4
Input: n = 3, edges = [[0,1],[1,2]]
Output: 0
Explanation:Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.

Example 2:

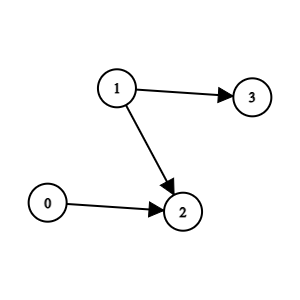
!https://assets.leetcode.com/uploads/2023/10/19/graph-4.png

1
2
3
4
Input: n = 4, edges = [[0,2],[1,3],[1,2]]
Output: -1
Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.

Constraints:

  • 1 <= n <= 100
  • m == edges.length
  • 0 <= m <= n * (n - 1) / 2
  • edges[i].length == 2
  • 0 <= edge[i][j] <= n - 1
  • edges[i][0] != edges[i][1]
  • The input is generated such that if team a is stronger than team b, team b is not stronger than team a.
  • The input is generated such that if team a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.

Solve

法1

用union find 的方法，但不一樣的是 並不是每一段都會連接

這題是為了找有最前面的頭

所以當已經輸過的人輸多少次都無關，需要的是前面贏過的人更新到新的冠軍

當有人多個都沒有輸過的人，find( u ) ≠ find( v ) 就 return -1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
				# 每個一開始都視為自己是冠軍
        parent = [i for i in range(n)]
        def find(u):
            if parent[u] == u :
                return u
            
            parent[u] = find(parent[u])
            return parent[u]
        def union(u,v):
            pu = find(u)
            pv = find(v)
            if pu != pv:
                parent[pv] = pu

        for u,v in edges:
            pu = find(u)
            pv = find(v)

            # 重點!!! 加上這個判斷式，讓子節點不更新
            if pv != v:
                continue

            union(pu,pv)

        p = find(0)
        print(parent)

        for i in range(1,n):
            if find(i) != p:
                return -1
        return p

由於find 會變成一個找下一個，所以這方法會很慢

法2

這題重點為觀察是否有人沒輸過

沒輸過的就是冠軍 → 但是可能有多個沒輸過的人，導致還找不到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# not optimization ，its the idea
class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        loser = [0]*n
        for edge in edges:
            loser[ edge[1] ] += 1
        
        count = 0
        res = 0
        for i in range(n):
            if loser[ i ] == 0:
                count += 1
                res = i
            if count >= 2 :
                return -1

        return res

Time complexity: O(n)

Space complexity: O(n)

優化

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        losers = set(range(n))  

        for edge in edges:
            loser = edge[1]
            losers.discard(loser)  

        if len(losers) == 1:
            champion = losers.pop()
            return champion
        return -1